CMPUT 229 - Computer Organization and Architecture I
Lab 3: BCD Multiplication
Creator: Nathan Ulmer
Introduction
In 1983 the index of the Vancouver Stock Exchange was reset after accumulating a large error. Over the preceding months the index collected an erroneous loss of roughly 25 points every month, leading to an overall deficit of 500 points, or half the value of the index. After an investigation, the error was found to be caused by the use of truncation rather than rounding in the program that updated the index. The large issue caused by this simple programming error shows the importance of controlling precision in financial and business computations.
Binary Coded Decimal (BCD) encoded numbers can represent any integer exactly, and to any degree of precision. If arithmetic is performed on BCD numbers, the precision used in the computation can be controlled exactly. In this lab you will be implementing addition and multiplication of BCD numbers of arbitrary length.
Binary Coded Decimal
Instead of representing integers in binary, we can represent each decimal digit separately using binary coded decimal (BCD). Each decimal digit maps to its corresponding 4-bit binary representation.
| Decimal Digit | 4-bit BCD Representation | Decimal Digit | 4-bit BCD Representation |
|---|---|---|---|
| 0 | 0000 | 5 | 0101 |
| 1 | 0001 | 6 | 0110 |
| 2 | 0010 | 7 | 0111 |
| 3 | 0011 | 8 | 1000 |
| 4 | 0100 | 9 | 1001 |
A single BCD encoded number can only represent numbers from 0 to 9. To represent larger numbers, we can use more than one BCD encoded digit. BCD encoded numbers use the following terminology. A range of 4 bits is called a nibble. A byte consists of two nibbles, a low nibble from bits 0 to 3, and a high nibble from bits 4 to 7. The lowest digit of a number is the digit with the smallest place value, while the highest digit of a number is the digit with the largest place value. For example, the lowest digit of the number 3496 is 6, while the highest digit is 3.
This lab uses the following format for variable length BCD numbers:
- The number is encoded as an array of bytes, with a single BCD digit encoded in both nibbles of each byte. Thus, each byte has two BCD digits.
- The lower nibble of the first byte contains the lowest digit of the number.
- Each higher digit is encoded in BCD format, then stored in the next highest nibble.
-
The number is terminated with the value
0xcstored one nibble higher than the highest digit of the number. -
Numbers contain no leading 0's, except for the number 0 which is
encoded as
0xc0.
Starting at address 0x10001000, the number 1234 is
stored as:
| Address | Value | High Nibble (bits 4-7) | Low Nibble (bits 0-3) |
|---|---|---|---|
| 0x10001000 | 0x34 | 0011 | 0100 |
| 0x10001001 | 0x12 | 0001 | 0010 |
| 0x10001002 | 0x0c | 0000 | 1100 |
Similarly, the number 98651 is stored at address
0x10001000 as:
| Address | Value | High Nibble (bits 4-7) | Low Nibble (bits 0-3) |
|---|---|---|---|
| 0x10001000 | 0x51 | 0101 | 0001 |
| 0x10001001 | 0x86 | 1000 | 0110 |
| 0x10001002 | 0xc9 | 1100 | 1001 |
Addition Algorithm
Given two BCD numbers A and B, to compute their sum add together the digits of A and B with the same place value. If any partial sum is greater than or equal to 10, propagate the carry. For example, the addition of the numbers 3902 and 4585 proceeds as follows:
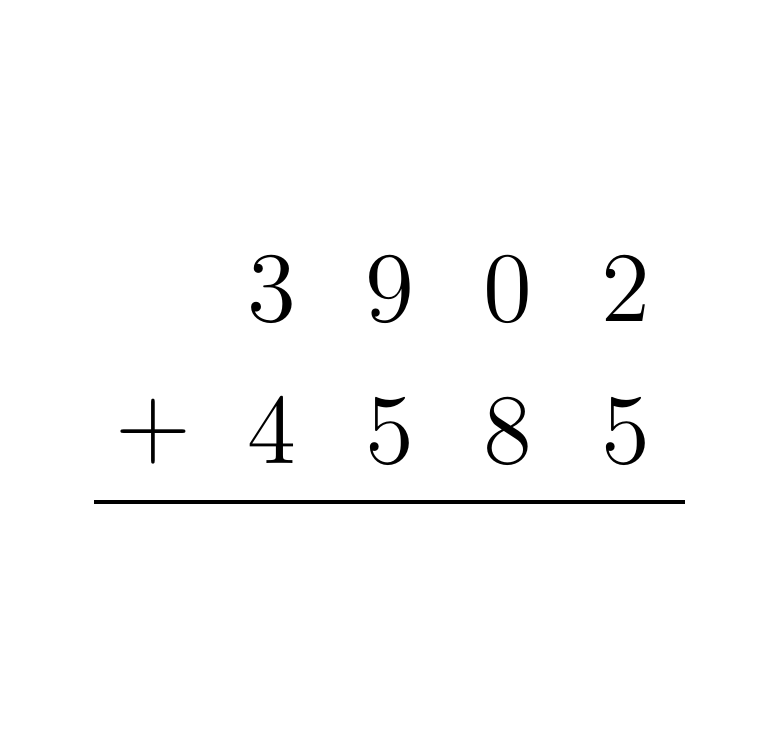
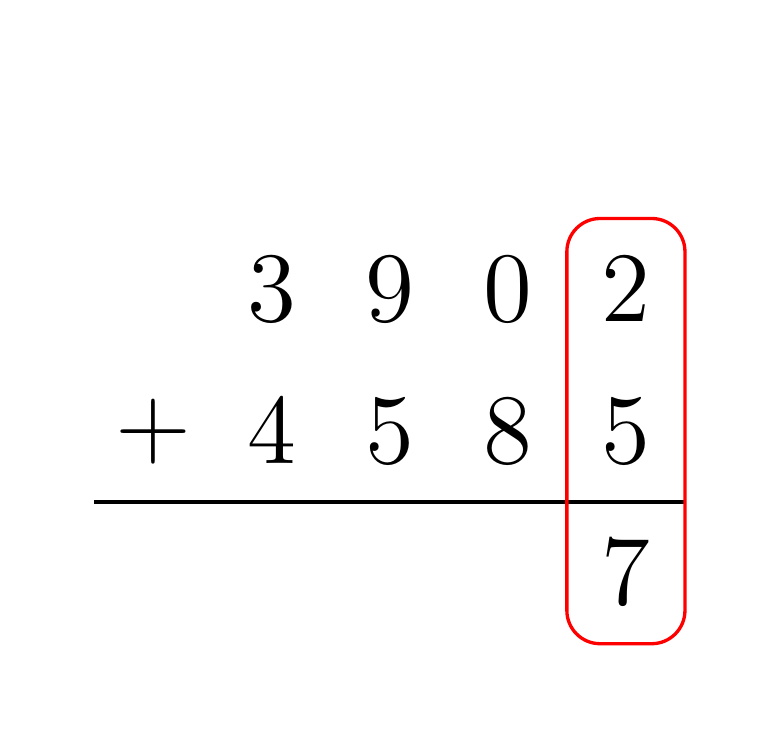
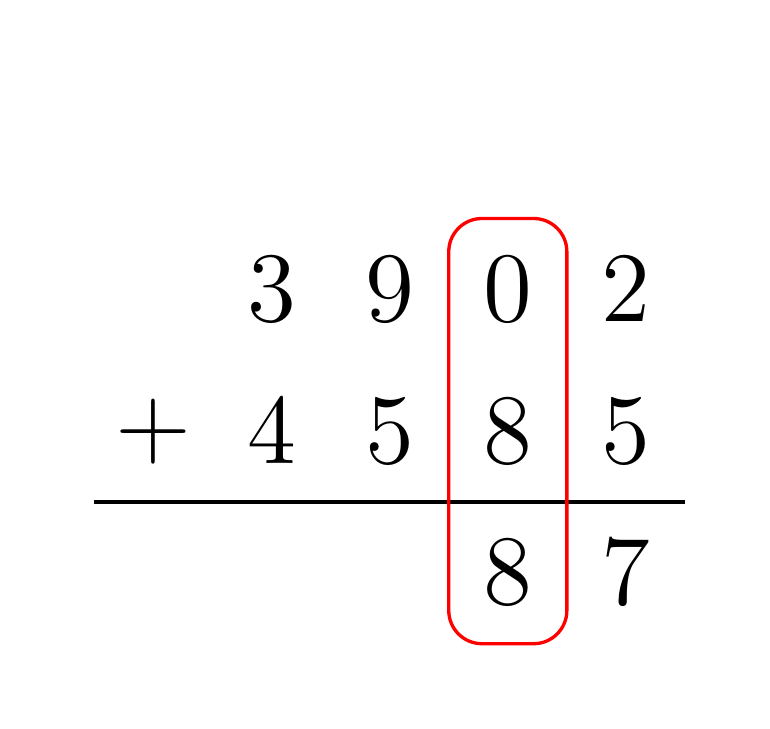

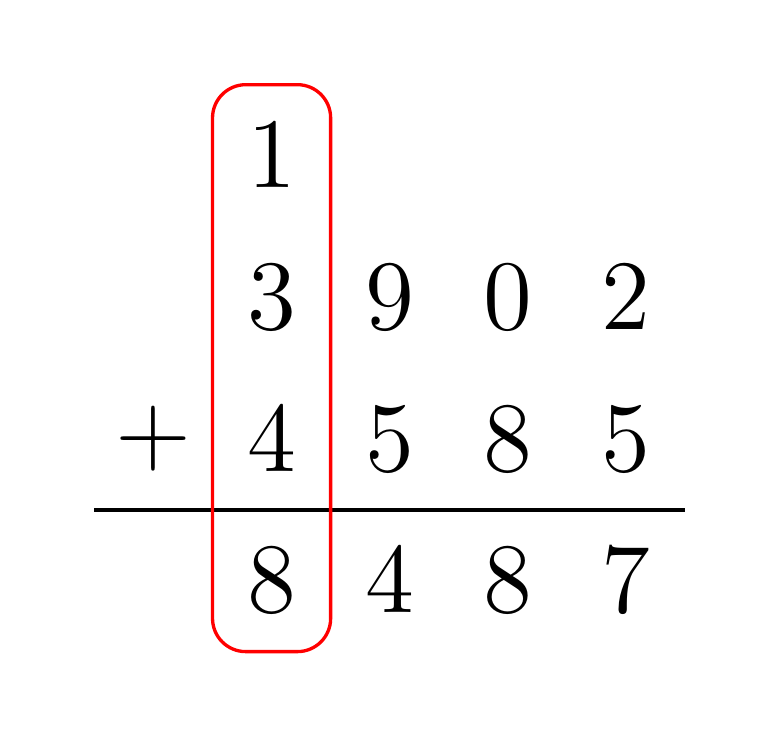
Multiplication Algorithm
Two BCD encoded numbers are multiplied using the long multiplication algorithm as follows.
Given two input numbers A and B, for each digit of B multiply that digit by each digit of A, and shift the result by the place value of B. When multiplying two digits together, be sure to propagate any carry to the next digit multiplication. Finally, each of the partial products must be summed. For example, consider the multiplication of 9429 by 385:
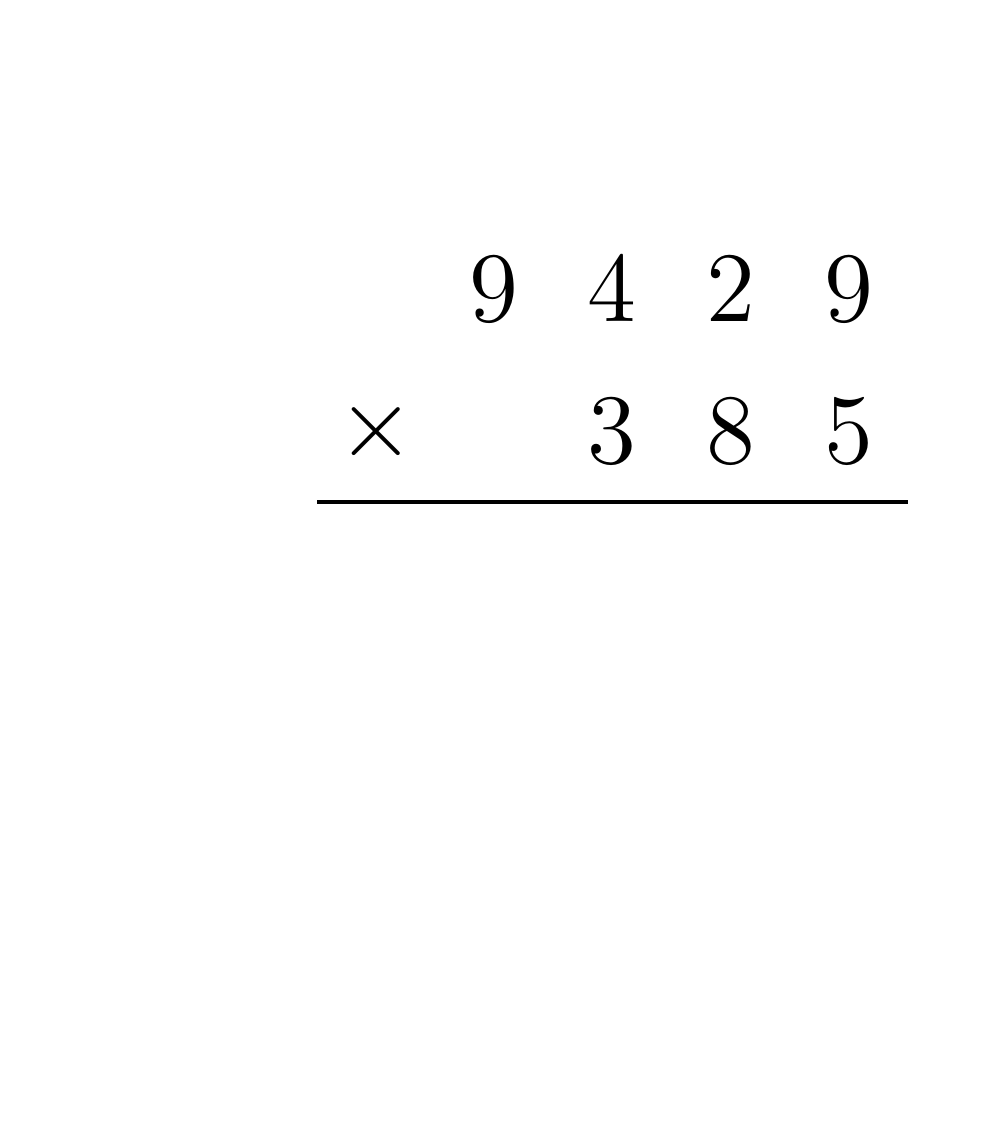
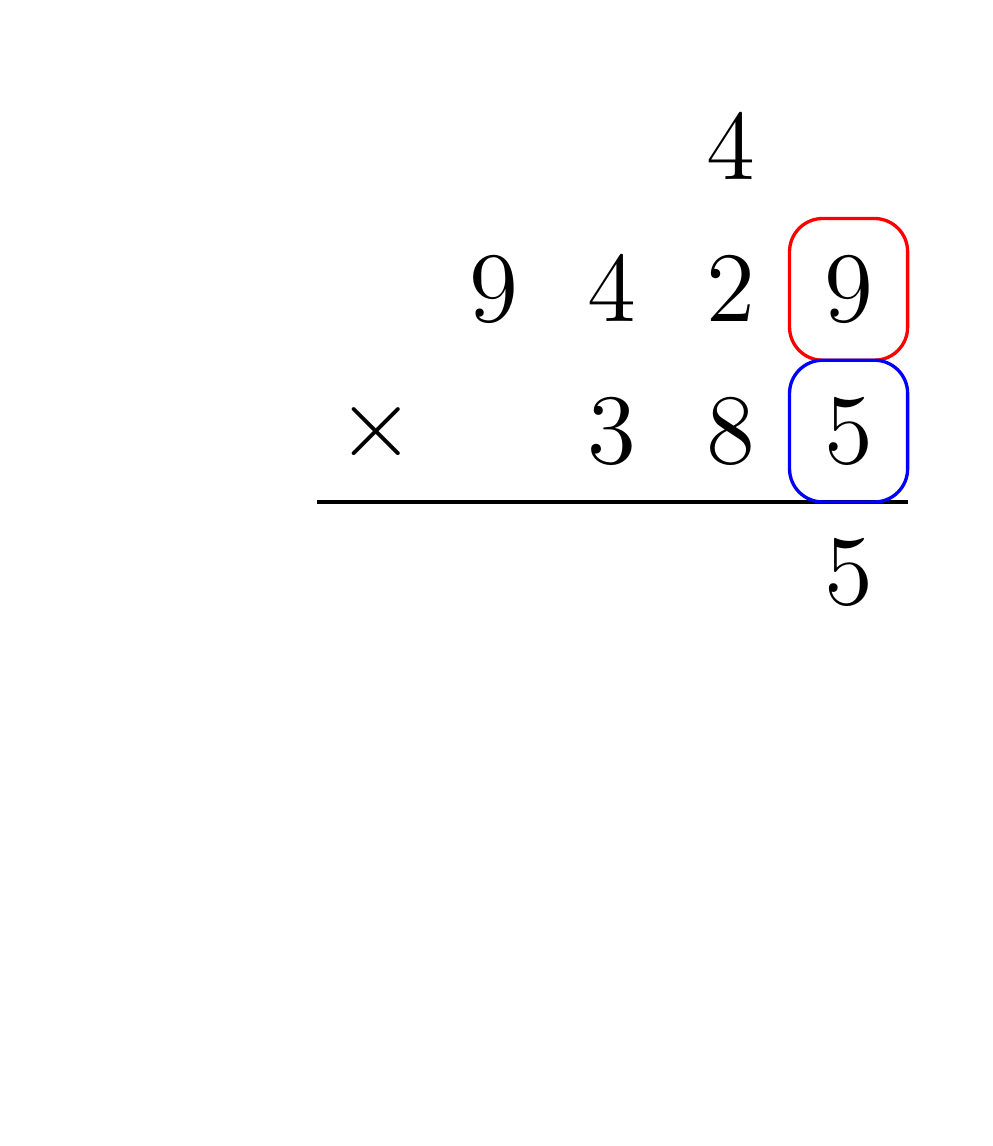
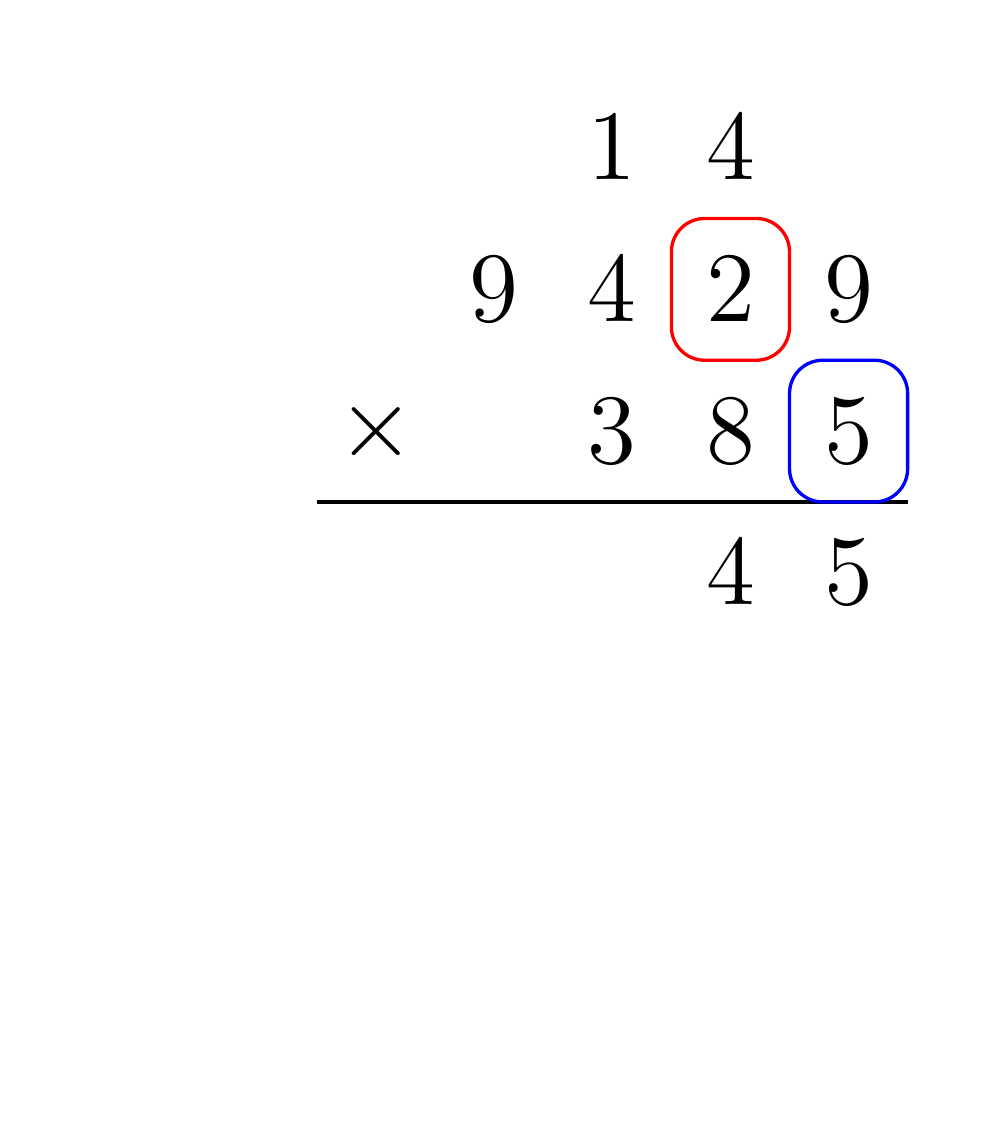
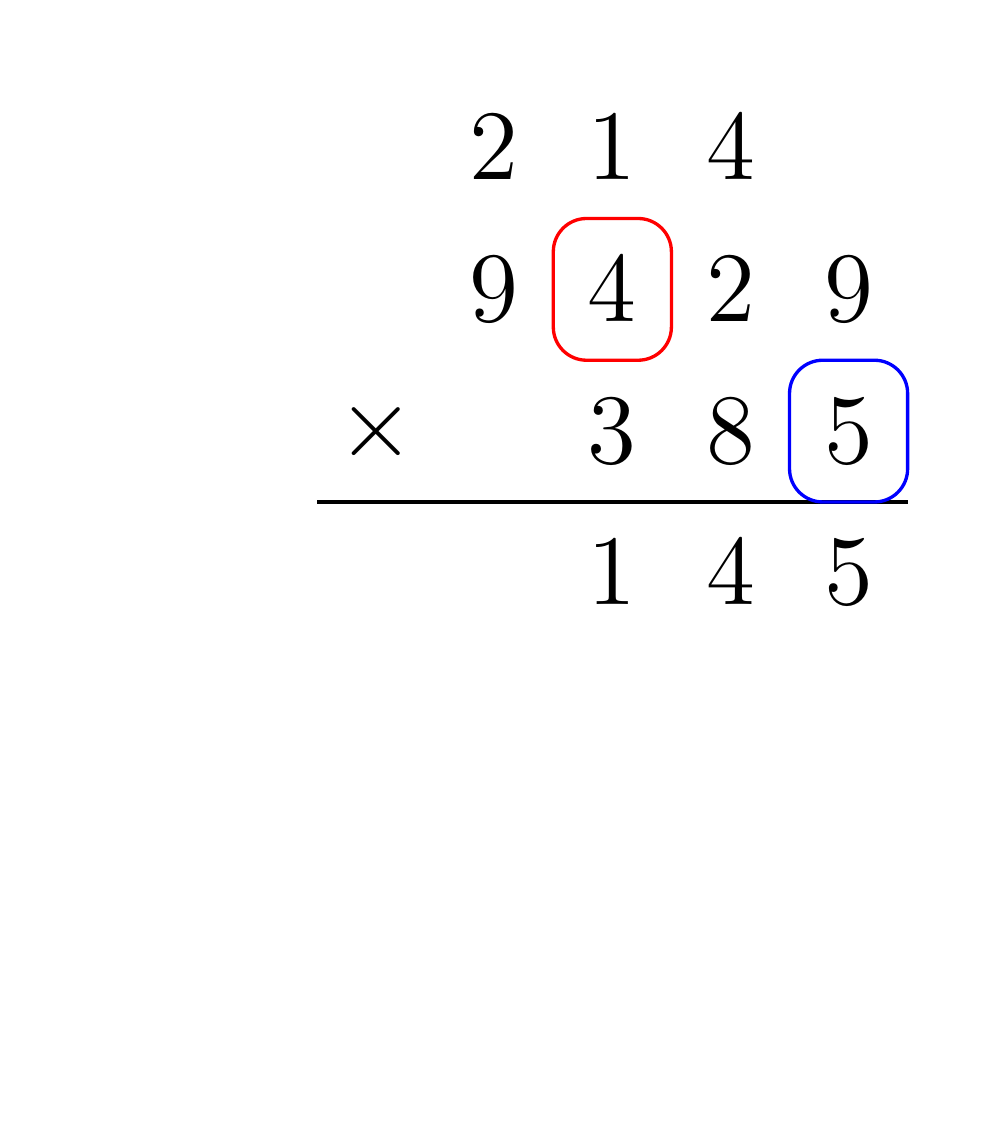
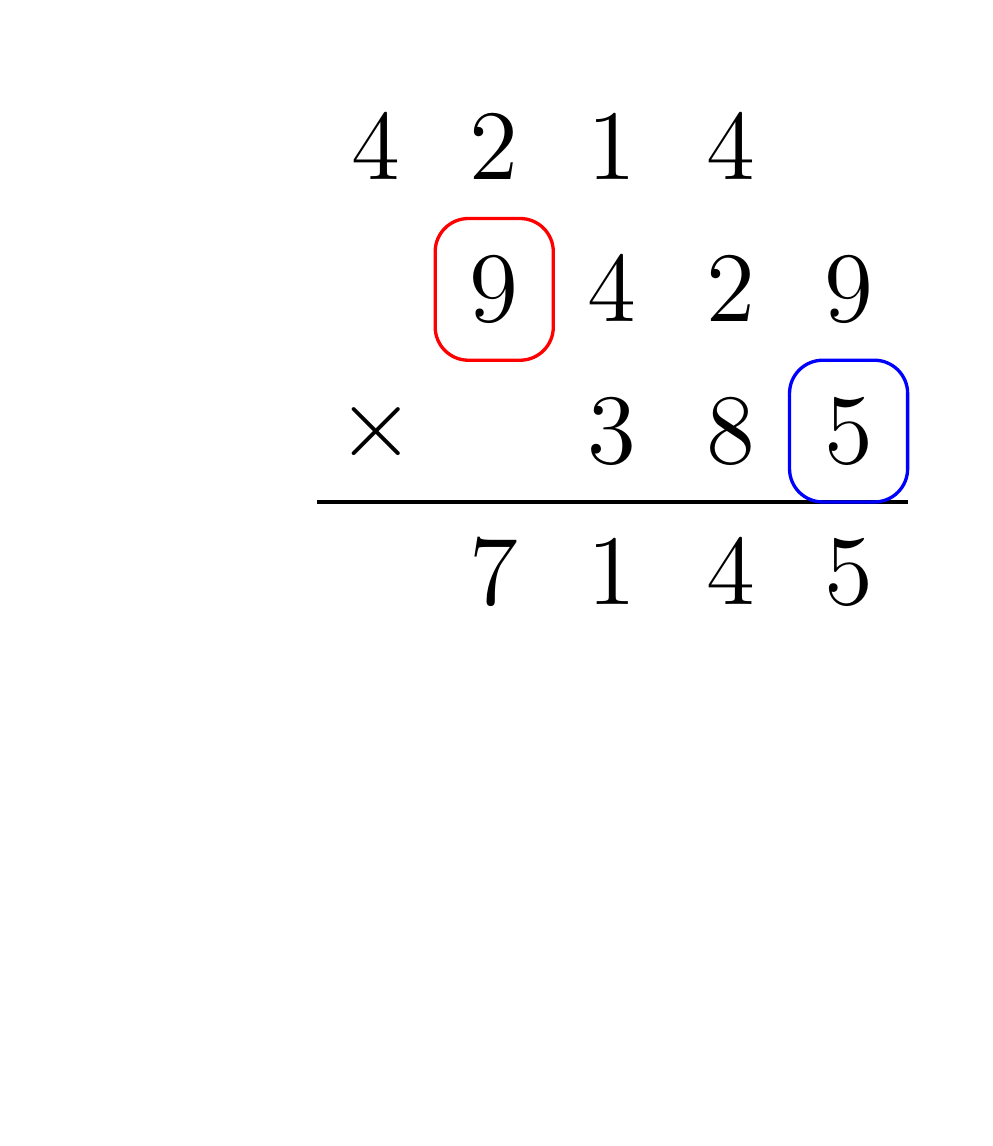

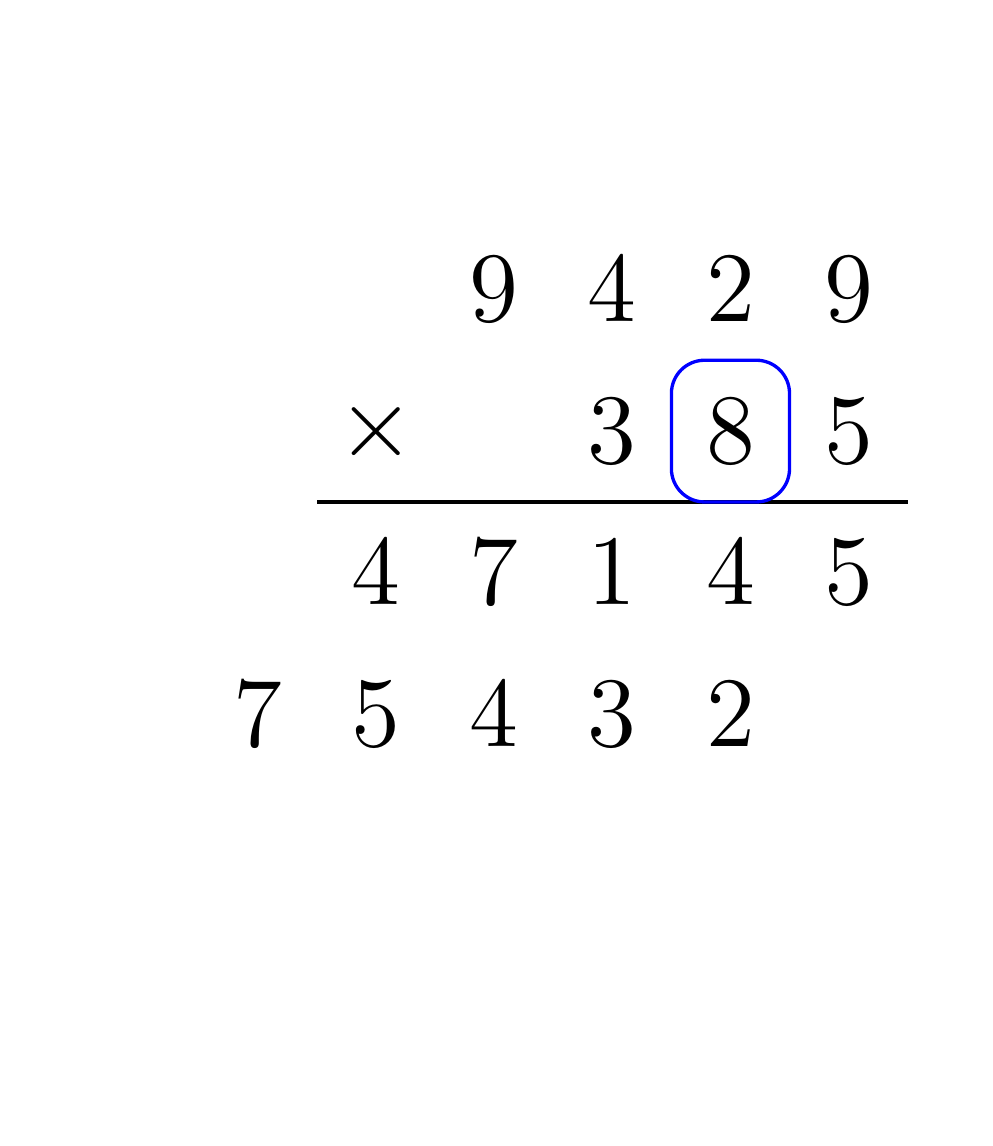
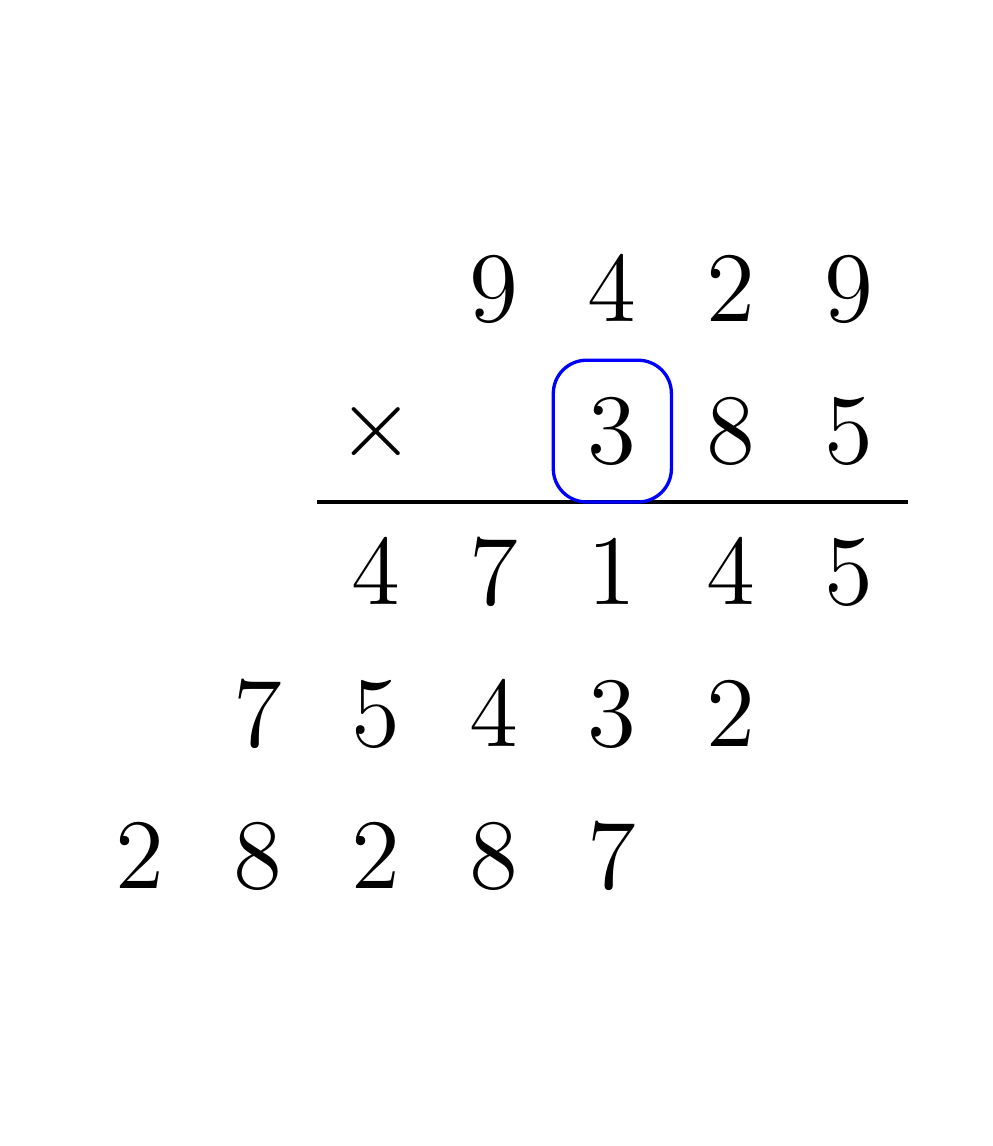
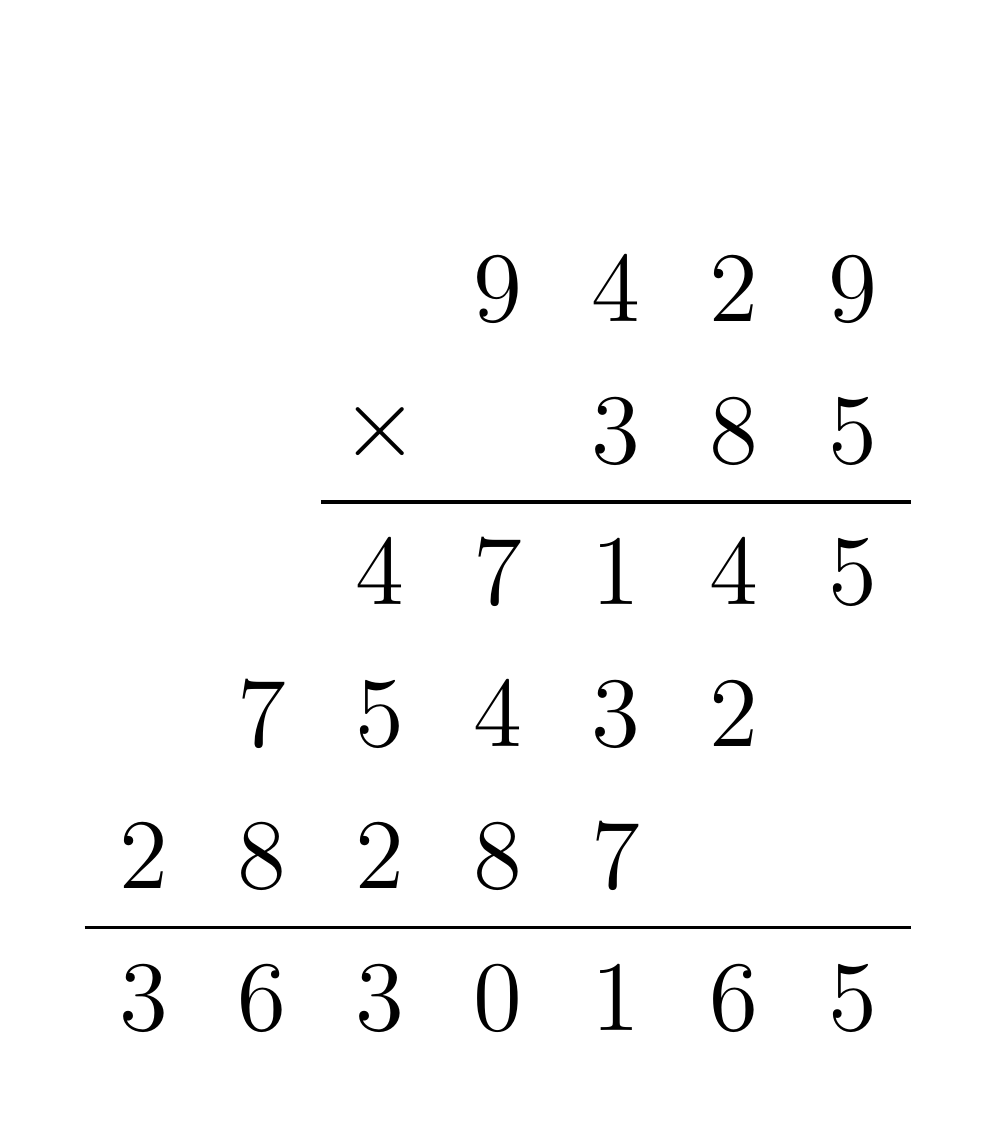
To implement the addition and multiplication algorithms in
RISC-V assembly you should consider the mul,
div, and rem
instructions.
Memory Allocation in RISC-V
A solution for this lab requires the use of buffers to store the results of intermediate computations. There are two types of memory allocations, static allocation and dynamic allocation. In this lab you are responsible for choosing the type of memory allocation to use as well as when to allocate.
Static Allocation
Static memory allocation requires that the size of the variables
be known before execution. Static memory allocation is done
using assembler directives in RARS. The
.data directive indicates that the subsequent lines
contain directives that reserve space for data. For example, the
following sequence statically allocates memory for a 64-byte
space and a single 32-bit word:
.data buffer: .space 64 word: .word 1
A full list of assembler directives can be found at the following link.
Dynamic Allocation
Dynamic memory allocation does not require the size of a variable to be known in advance. This allows for flexibility when handling inputs of unknown sizes, such as a string.
In RISC-V, dynamic memory allocation is accomplished through a
system call: ecall. The register
a7 contains the code indicating what the system
call should do. To allocate memory, set a7 to 9.
The register a0 specifies the amount of contiguous
memory allocated, in bytes. After this ecall the
address of the newly allocated memory will be in
a0.
For example, to dynamically allocate a buffer of 50 bytes we can use the following code:
li a0, 50 # 50 bytes to allocate li a7, 9 # ecall for memory allocation ecall # a0 <- Pointer to new memory
Assignment
This lab implements a series of function to multiply two BCD numbers. You are required to implement all of the following functions:
mulBCD
This function multiplies two numbers A and B, and prints the result.
Internally, the multiplication must be performed on binary BCD numbers. This
function is called from common.s.
Arguments:
a0: pointer to an ASCII encoded integer (A).
a1: pointer to an ASCII encoded integer (B).
Returns:
N/A
Note that mulBCD takes in two strings as input.
addBCD
This function adds two BCD numbers in binary format, and stores the sum into a
buffer. The sum is stored as a binary BCD number.
Arguments:
a0: pointer to the first operand as a binary BCD number.
a1: pointer to the second operand as a binary BCD number.
a2: address of the result buffer.
Returns:
N/A
readBCD
This function reads in an string and writes the number in the BCD format into
a buffer.
Arguments:
a0: pointer to an ASCII encoded integer.
a1: pointer to a result buffer.
Returns:
N/A
printBCD
This function prints a BCD number to standard output. A newline ('\n') should
be printed after the number. Assume that the input number has at least one
digit.
Arguments:
a0: pointer to an integer in binary BCD format.
Returns:
N/A
Helper Functions
To help you write your solution, we have provided the following
functions in the common.s to operate on binary BCD
numbers. These functions allow you to get and set individual BCD
digits, as well as find the length of a binary BCD number.
getNth
Get the nth digit of a binary BCD number. The lowest digit has index 0.
Arguments:
a0: pointer to a binary BCD number
a1: index of the digit to get
Returns:
a0: nth digit
setNth
Set the nth digit of a binary BCD number. The lowest digit has index 0.
Arguments:
a0: pointer to a binary BCD number
a1: index of the digit to set
a2: digit to set the given index to
Returns:
N/A
length
Get the length of a binary BCD number, including the terminating character.
Arguments:
a0: pointer to a binary BCD number
Returns:
a0: Length of the input number
To understand how these functions work, consider the the number
12345. In the binary BCD number format, this number is stored as
three bytes, being
0x45, 0x23, 0xc1. If a pointer to this number is in
s0, then the following instruction stream will have
the given results.
mv a0, s0 li a1, 1 # Get the 2nd digit jal getNth # a0 <- 4 mv a0, s0 li a1, 4 # Set the 4th digit li a2, 9 # Set to 9 jal setNth # Number is now 92345 mv a0, s0 jal length # a0 <- 6 (5 digits + terminator)
Writing a Solution
The assembler directive .include "common.s" at the
start of the solution file causes the assembler to insert the
code present in the common.s file at the start of
the solution. The code in the common.s file reads
the program arguments, and loads the corresponding file. This
file is then parsed and given to mulBCD as input.
The common.s serves as the entry point, and takes
care of calling mulBCD with the correct arguments.
Take care to include a return statement at the end of the
mulBCD function to return control to the
common.s file.
Be sure to follow the RISC-V register calling conventions for
all functions in your solution. Arguments to functions should be
passed in the a0-a7 registers, and any return
values should also be returned through registers
a0-a7.
We recommend that you write the functions of your solution in the following order:
printBCDreadBCDaddBCDmulBCD
Testing your Lab
Test cases are plain text files with the following format:
[number 1] [number 2]
Where numbers 1 and 2 are strings of the characters 0 to 9, with
no leading zeros. To run a test, enter the full path of the test
file into the program arguments.
Check My Lab
This lab is supported in
CheckMyLab. To
get started, navigate to the BCD-Multiplication lab in
CheckMyLab found in the dashboard. From there, students can
upload test cases in the My test cases table. Test cases
are text files which follow the format described above.
Additionally, students can upload their
multiplyBCD.s file in the
My solutions table, which will then be tested against all
other valid test cases.
Resources
Notes and Assumptions
-
The input strings to given to
mulBCDconsists only of the digits 0 to 9, and will have no leading 0's. (Except for the number 0) - Numbers in the binary BCD format should never have leading zeros (except for 0).
- The input numbers will have less than or equal to 100 digits.
- All input numbers will have at least one digit.
-
If you get the error
ERROR: Couldn't open specified file, give the full path to the test file in the program arguments.
Marking Guide
Assignments too short to be adequately judged for code quality will be given a zero for that portion of the evaluation.
- 30% for
mulBCDand overall correctness. - 30% for
addBCD. - 10% for
printBCD. - 10% for
readBCD. - 20% for code cleanliness, readability, and comments.
Submission
There is a single file to be submitted for this lab.
multiplyBCD.s should contain the code for your
solution.
-
Do Not add a
mainlabel to this file. -
Do Not modify the line
.include "common.s". -
Keep the file
multiplyBCD.sin theCodefolder of the git repository. - Push your repository to GitHub before the deadline. Just committing will not upload your code. Check online to ensure your solution is submitted.
