CMPUT 229 - Computer Organization and Architecture I

Lab 3: Data Compression

Introduction

As the amount of information sent through the internet rapidly increases, it is crucial that this data is represented as efficiently as possible. When you upload or send something online, it will practically never be transported in the same form as it exists on your device. It will be compressed to take less bandwidth for transmission and less memory in routers. Compression is a process through which data is made smaller and decompression is the reverse process in which compressed data is reconverted into its normal, usable, form once it reaches its destination.

Background

Lossless data compression is the process of taking in an input file of data, transforming it, then returning an output file that is shorter (is composed of fewer bytes) than the input file and contains all of the information needed to convert it back to the original input file. Lossy compression, however, converts data into a much smaller form than can be achieved by lossless compression at the cost of accuracy or resolution. Lossy compression is appropriate for mediums such as video streaming, where a high-resolution video may be sent at a lower resolution without issue. Lossless compression, however, is needed for sending data that cannot be changed even slightly, such as text files; removing letters in a book is not an acceptable compromise for reducing size. In many situations a file of data is compressed, transmitted, and decompressed.

Task

In this lab, you will write important functions for a simple implementation of an approach to lossless compression called dictionary compression.

Tables in Memory

A table in assembly is a collection of values stored in a known amount of allocated space with a known base address. The size of the elements in a table, as well as the offset between the address of an element and the beginning of the table, are also known. The base address and offsets can then be used to access an element at a given index. It is often helpful to correlate two (or more) tables, meaning that each element in one table is linked to a related element in another table (similarly to how a dictionary data structure links a key element to a value element). There are generally two ways to correlate tables: index correlating, where the tables are stored in distinct memory locations, and elements sharing the same index are linked, or spacially correlating, where both tables are stored in the same memory area, and elements from one table are immediately followed by the linked element from another table. As a rule, for large tables of differing alignments, for instance a table containing words versus a table containing bytes, it is more efficient to index-correlate than to allocate extra space or to deal with unaligned word issues. If the alignments of all of the entries match, it is more efficient to spacially-correlate. In this lab, you will be implementing index-correlated tables, although it would be also possible to execute this lab using spacially-correlated tables.

Dictionary Compression

Dictionary compression reduces the space need to represent repeated data items in a file. When a segment of a sequence occurs frequently, a copy of it is added to a table referred to as the dictionary. To compress the sequence, replace each occurrence of that segment with a reference to its index in the dictionary holding this item. In general, these segments can be of arbitray length. Therefore, replacing a long segment of characters with a single number can make the overall sequence shorter. In this lab the size of the segments is fixed and is equal to one four-byte word.

In order to achieve compression, segments added to the dictionary should occur multiple times in the sequence. This is because in order to decompress the sequence, the decompressor will need to have access to the dictionary. Therefore, the dictionary is sent alongside the compressed sequence in the output, and the size of the dictionary should be as small as possible while allowing as much compression as possible for the sequence. For example, consider input data that contains no repetitions. Naively storing every segment in the dictionary, could make the dictionary as large as the original sequence and the "compressed" output could take more bandwidth to send than the original uncompressed sequence.

Compression Format

In order for a dictionary, encoder, and decoder to work with one another, it is necessary for each of them to conform to certain format conventions. In real-world compression algorithms, these different formats are indicated by the extension of a file compressed by that algorithm (e.g. .xz, .lzma, .7z). For your output to be graded correctly, it will need to follow the format rules specified in this page.

Words

The input data is a sequence of 4-byte words. In RISC-V, words are 4 bytes long and therefore consist of 4 ASCII characters. These words are the units that you will be storing and replacing as described in the following sections. All input provided to your functions will have a size in bytes that is a multiple of 4. The end of the file is signalled by the sentinel word 0.

Word and Count Tables

Building this dictionary requires knowledge about the number of occurrences of any unique word in the input. For this purpose, you will be generating two index-correlated tables:

• a wordTable contains each unique word in the input exactly once, in the order in which they first appear in the input;
• a countTable contains the number of times (stored as a byte) for each word in wordTable.

In all test cases, the same word can appear at most 255 times so that the number of times can fit in one byte. The wordTable should not contain the end-of-file sentinel word, and your tables should not be null-terminated nor contain any null bytes or words.

Dictionary

The dictionary is built from the wordTable and countTable. In this lab, a function that builds the dictionary is provided to you. The dictionary can contain up to 128 elements and therefore a reference to any index in the dictionary takes 7 bits. The first entry in the dictionary has index 0. The most significant bit of the byte used to index the dictionary is reserved to signal that the byte represented a compressed word as explained later. Each element of the dictionary is a word from the wordTable provided to it. The dictionary will most likely not contain all of the words in wordTable, as it is designed to only contain the words that will be the most valuable for encoding.

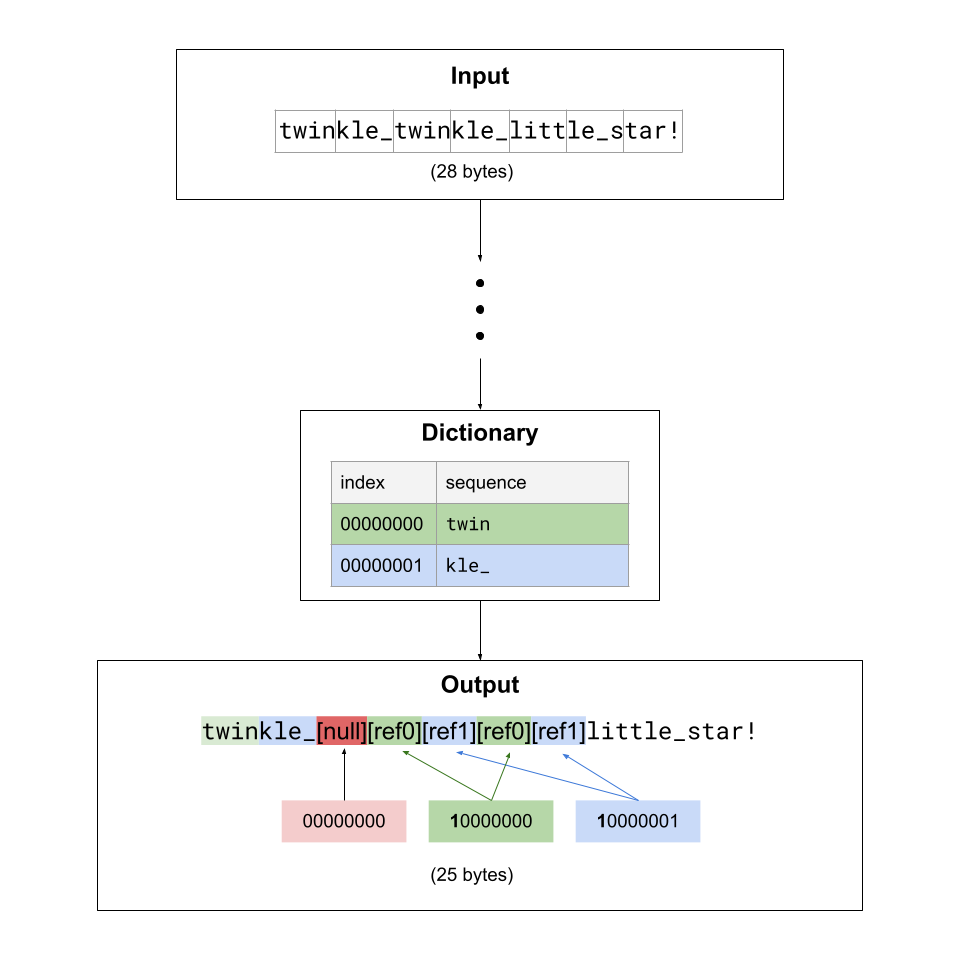
In this example the words in the input contains characters from a string. The words are surrounded by grey boxes.

Encoding

The encoding algorithm replaces words that are in the dictionary with a special byte referencing the dictionary entry. Encoding also adds the dictionary to the start of the output.

Generating the Compressed Sequence

All ASCII characters are represented by numbers from 00000000₂ (0₁₀) to 01111111₂ (127₁₀). Notice that all ASCII characters have a 0 in bit 7. Since the dictionary can hold up to 128 elements, the dictionary indices are also from 00000000₂ (0₁₀) to 01111111₂ (127₁₀). To differentiate a dictionary-reference byte from a regular ASCII character, reference bytes have a 1 in bit 7, and the 7 remaining bits in the byte are the index of the dictionary element where the relevant word is stored. For example, a word from the input that is also stored in the dictionary at index 00000101₂ will be replaced in the compressed sequence with the byte 10000101₂.

A dictionary reference byte contains the index of the element in the dictionary containing the word, not the offset of the byte at which the word begins in the dictionary. Each dictionary element is 4-bytes long. For example, the first byte of element 5 begins at byte offset 20. A reference to this word would reference index 5, not position 20.

Words that do not have a match in the dictionary appear unchanged in the compressed sequence. Given the replacement of some 4-byte words with single-byte dictionary references, words in the space provided for you to store your output may not be aligned to the word boundary, preventing you from using sw. Therefore, all words must be written to the output byte by byte. Because of endianness, the bytes within a word loaded from the input must be stored to the output in reverse order. For example, say that you use lw on the input to obtain the word "le_s". This word does not have a match in the dictionary, so it must be stored to the output as-is, byte by byte, in reverse order. Therefore, you would use sb to store the "s" character byte, then "_", "e", and "l", ultimately storing "s_el" to the output. If you were to then load the following word "tar!" which also doesn't have a match in the dictionary, you would repeat this process and store "!rat" to the output, altogether having stored "s_el!rat".

Finally, the compressed sequence must end with the end-of-file sentinel word found at the end of the input, meaning that the last 4 bytes must each be 00000000₂.

Outputting the Dictionary

There are many ways to share the dictionary with the decoder. The format for this lab requires that you add every word in the dictionary consecutively to the beginning of the output, before the compressed sequence. To signal the end of the dictionary and the beginning of the compressed sequence, you will add a null (00000000₂) byte after the last byte of the dictionary. Following this byte will be the compressed sequence as described above. The end-of-file sentinel word at the end of the compressed sequence signals the end of the overall output file.

Format Summary

Word and Count Tables

• wordTable contains each unique word from the input exactly once, in the order that the words first appeared in the input
• countTable contains the count representing how many times any word in wordTable occurred in the input, in the same order as in wordTable
• countTable has a 1-byte element for each 1-word element in wordTable (meaning that wordTable should take exactly 4 times more space than countTable in memory)
• neither table should contain any null bytes

Dictionary

• The dictionary has at most 128 elements (i.e. the largest allowed dictionary has indexes 0 to 127);
• Each dictionary element contains a word from the input;
• These two properties imply that the largest allowed dictionary has a total size in memory of 512 bytes.

Encoding

• The output begins with the entire dictionary, followed by a null character byte;
• The compressed sequence follows immediately after the null character;
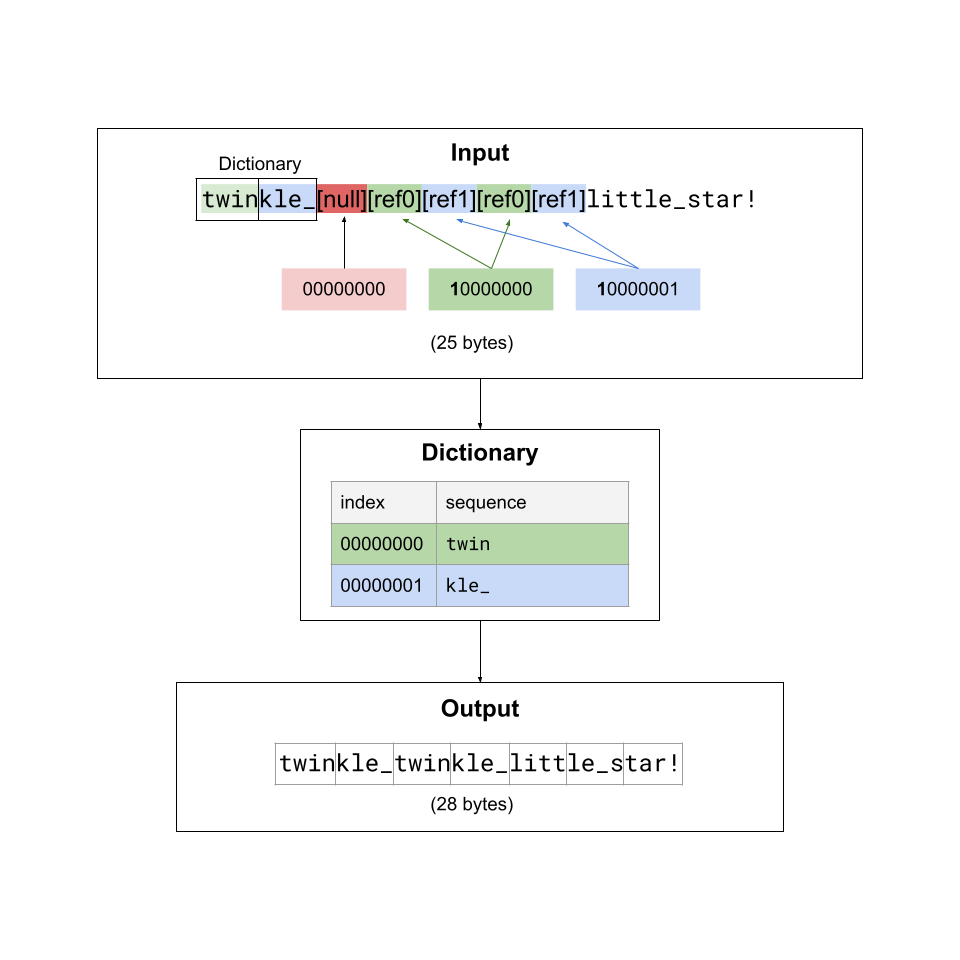
• Words from the input that have a match in the dictionary are replaced with the reference byte for that word in the compressed sequence;
• Reference bytes have a 1 in bit 7 and bits 0-6 contain the index of the dictionary element in which the word can be found;
• Words in the input that do not have a match in the dictionary are added to the compressed sequence normally;
• The compressed sequence ends with the end-of-file sentinel word 0, also signalling the end of the output.

Decoding

The decoder uses the dictionary portion of the file to lookup dictionary reference bytes. You do not need to implement a decoder in this lab. A decoder is provided in binary form for you to use to test your encoding.

Assignment

The solution for this assignment consists of a RISC-V assembly file containing three functions that perform the encoding as specified:

• buildTables
• Given the contents of an input stored in memory, builds a wordTable containing one of each unique word in the input, as well as an index-correlated countTable that contains the number of occurrences of each word in wordTable
• Arguments:
• a0 = the address of the contents of a valid input in memory terminated by the end-of-file sentinel word.
• a1 = the address of pre-allocated memory in which to store the wordTable.
• a2 = the address of pre-allocated memory in which to store the countTable.
• Return Values:
• a0 = the number of elements in either table.
• encode
  • Given the contents of an input and a dictionary for that input, generates encoded output that conforms to the format.
  • Arguments:
  • a0 = the address to the contents of a valid input in memory terminated by the end-of-file sentinel word.
  • a1 = the address of a dictionary table in memory.
  • a2 = the number of word elements in the dictionary.
  • a3 = the address of pre-allocated memory in which to store the output.
  • Return Values:
  • a0 = the size of the output in bytes (not including the end-of-file sentinel at the end).
  • The grading script may test this function using a dictionary that were generated without running your buildTables function. Thus, this function must not rely on any global variables written to by buildTables.

Input Guarantee

• The input is at most 1024 bytes large.
• The input file's size is a multiple of 4.

Testing

The Code directory contains the following files:

• compression.s: this is where you will write the code for the buildTables and encode functions. You can run test cases on your solution by passing the name of the test file (including ".txt") as an argument into RARS.
• common.s: loads an input file at the path provided as a program argument, calls your buildTables function and writes your tables to tables.txt, then calls buildDictionary with your tables as arguments, and finally calls your encode function using the generated dictionary as an argument and writes the output to encoding.txt.
• decode.o: a compiled C program that can decode the encoding.txt file generated by common.s using your solution.
• print-encoding.o: a compiled C program that can print the encoding in encoding.txt in a more human-readable format.
• print-tables.o: a compiled C program that can print the tables in tables.txt generated by common.s using your solution.

Resources

• Slides used for in-class introduction of the lab (.pptx) (.pdf)
• Video Recording for Introduction to the Lab - GoogleDrive YouTube

Marking Guide

Assignments too short to be adequately judged for code quality will be given a zero for that portion of the evaluation.

• 30% For correctly building word and count tables
• 50% For correctly encoding the input file
• 20% For code cleanliness, readability, and comments
• Here is the mark sheet used for grading

Submission

There is a single file to be submitted for this lab:

• compression.s should contain the code for the functions buildTables and encode
• Do not add a main label to this file
• Do not modify the line .include "common.s"
• Keep the file compression.s in the Code folder of the git repository.