University of Alberta logo

CMPUT 229 - Computer Organization and Architecture I

Lab 3: Expression Parser

Creator: Arsh Ahsan

Introduction

As programmers, a lot of code is written in high-level languages. This course exposes students to low-level languages such as assembly in RISC-V. It would be natural, then, to wonder how this transition from a high-level language to a low-level language happens. The most common way this is done today is by using a compiler, which is a program that converts a high-level language into a low-level language.

Background

Compilers are composed of several parts, one of which is called the parser. This part of the compiler is able to take a program and create a data structure known as an Abstract Syntax Tree. In some parsers, this is done by a technique called Recursive Descent. As its name suggests, it recursively breaks down a program into several smaller parts, and then puts them together in a way that allows another program to traverse the resulting tree. This is helpful for analyzing the program and evaluating statements and expressions. In another kind of program, commonly referred to as an interpreter, an expression is evaluated directly instead of being a part of an Abstract Syntax Tree.

There are several techniques used in parsers when evaluating expressions, but the one that will be the focus of this lab will be a technique known as Precedence Climbing. This algorithm recursively evaluates an expression depending on the precedence of the operators in the expression, and returns each part of the expression, piece by piece, evaluating these pieces together to get the result of the whole expression.

Task

This lab involves writing a program that takes in a file with an expression that contains arithmetic, logical, and bitwise operators, as well as unary operators, and returns the result of the expression using the Precedence Climbing algorithm.

Tokenization

Tokenizing (or lexing) is the process of converting a string of characters into a sequence of tokens with some kind of meaning attached to them. This process is done before parsing so that the parser has the minimum amount of information that can "explain" the entire expression.

In this lab, it will not be required to implement a tokenizer, and the tokenize function is already provided. However, understanding how tokens are implemented in this lab is necessary to complete it.

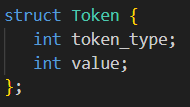
A Token can be thought of as a C struct that contains two elements: a token type, and the token's value. The only tokens that contain values in this lab are the integer tokens. All other token types will only contain the token type.

token C struct

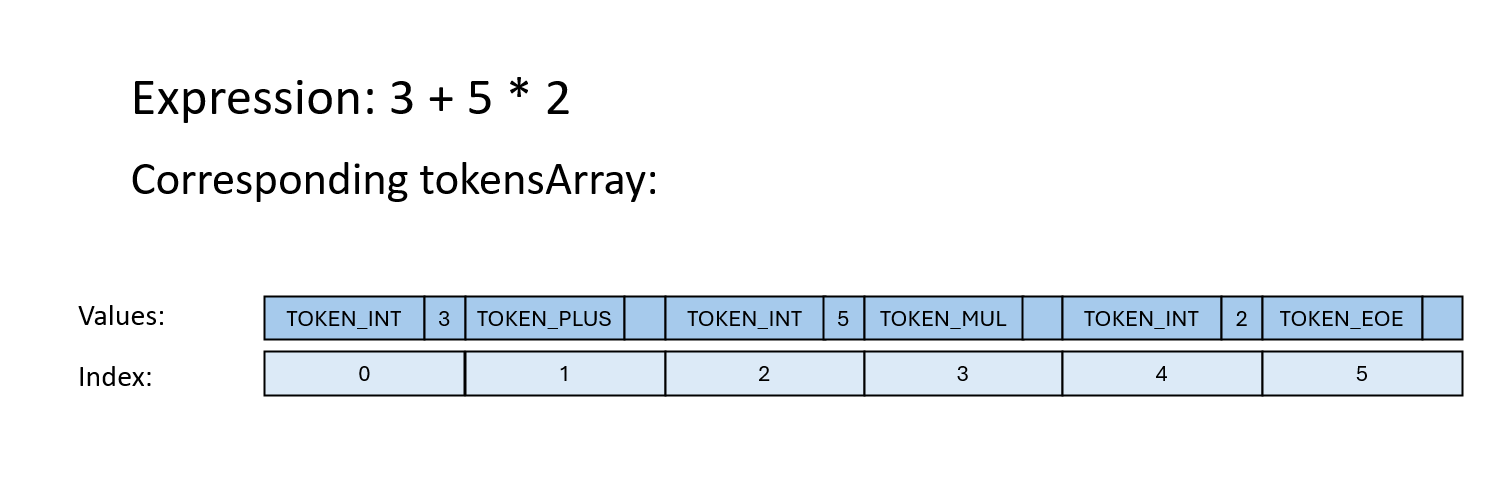
The tokensArray variable will contain the tokens for this lab.

At the end of tokensArray is a token with type TOKEN_EOE (End of Expression), which signifies the end of the tokensArray.

tokens array example

Note that a token is made of two 32-bit words. As such, the maximum value for an integer would be 231 - 1, and the minimum would be -231. There may be some operations that lead to values greater or less than these. When this happens, it is referred to as integer overflow (and likewise, integer underflow, for less than the minimum value). This lab does not require handling overflow/underflow checking to be implemented in the solution.

Parsing

Abstract Syntax Tree

As mentioned above, a parser in a compiler converts a program's source code into an Abstract Syntax Tree. A Tree is a data structure that consists of nodes, which can contain any kind of data. Every node in a tree has a Parent node, i.e. a node that connects to another node, except for the Root node, which has no parent.

While a typical AST may contain several different kinds of nodes, for the purposes of this explanation, it can be assumed that every node is a Binary Operator node, which contains a left operand, a right operand, and a binary operator.

AST node example

When evaluating an expression using precedence climbing, an AST is collapsed from the bottom operand up to the top, which is why it can be referred to as a bottom-up algorithm.

This is a visual representation of what the algorithm should be doing:

Precedence

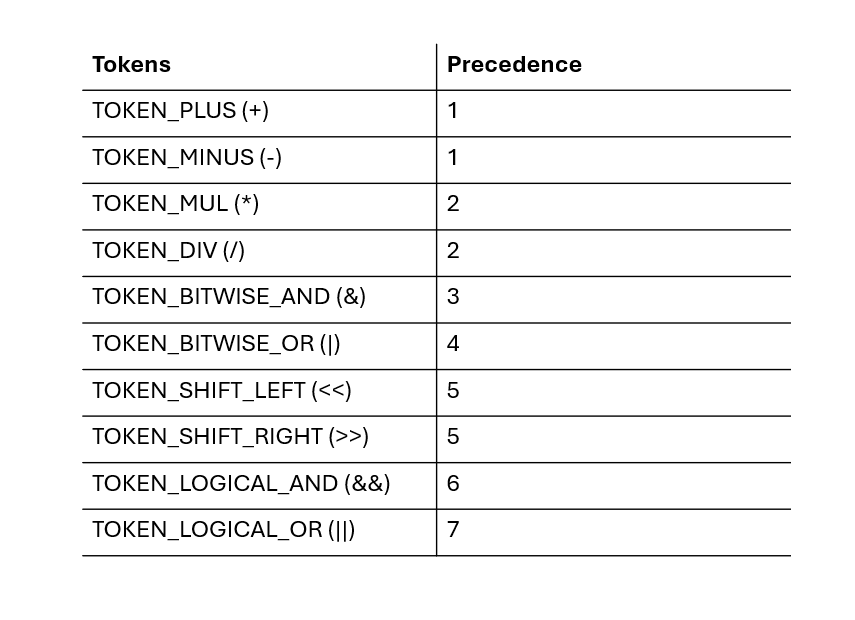
Each operator in this lab has a "precedence" level, i.e. a value that says when the binary expression should be evaluated. The lower an operator's precedence, the later in the evaluation the expression is evaluated.

Precedence in arithmetic operators follows the same precedence as in regular arithmetic; multiplication and division are both calculated before addition and subtraction. The precedence for the logical and bitwise operators are treated similiarly. A bitwise AND has a higher precedence than multiplication/division, and therefore is performed before multiplication/division. Next is a bitwise OR, which has a higher precedence than a bitwise AND. A left and right shift both have the same precedence, and said precedence is higher than a bitwise AND. A logical AND comes next, and then a logical OR.

The precedence used in this lab is different from the precedence used in several high-level languages, such as C or Python. As such, parsers for those languages will not be usable to test the results of expressions.

While binary operators are assigned a precedence that says when their expression should be evaluated, a unary operator does not need precedence, unary operators should be evaluated from the innermost to the outermost unary operator.

Below are examples of how unary operators are evaluated

  • -!~0
    1. -!(-1)
    2. -0
    3. 0
  • ~!-0
    1. ~!0
    2. ~1
    3. -2
precedence table

Associativity

When two operators of the same precedence are in succession to each other (such as 1 - 2 + 3), the order in which they are evaluated is determined by the associativity of the operators. If an operator is left-associative, then the left operator of successive operators in an expression is evaluated first. If an operator is right-associative, then the right operator of successive operators in an expression is evaluated first.

Most operators are left-associative, such as arithmetic, bitwise, logical, and comparative operators. Common examples of right-associative operators would be exponentiation, and the assignment operator (=) in C.

In this lab, all the operators are left-associative, meaning when two operators of the same precedence come one after the other, the left operator is evaluated first. With the example given above, 1 - 2 + 3 is evaluated as ( 1 - 2 ) + 3, which evaluates to 2.

Precedence Climbing

The algorithm begins by first parsing a factor, which can be an integer, along with 0 or more unary operators, or an expression, starting with an open paranthesis, with zero or more unary operators. This will be the left operand of the expression. After parsing this, the algorithm checks the next token in the tokens array. In a valid expression, this would be an operator. Here, the precedence function is called, which returns the precedence of the operator. The operator's precedence is compared to the current precedence.

The precedence for the closing parenthesis ')' (TOKEN_CPAREN) and the end of expression token (EOE) is both set to -1. This ensures that the condition if op_prec < current_prec in the pseudocode will always be true whenever these tokens are encountered. As a result, there is no need to explicitly check for ')' or EOE tokens in the condition.

If the current precedence is greater than the precedence of the operator, or the token is a closing parenthesis, the expression must break and return its result, as the next expression must now be evaluated. Otherwise, the algorithm continues. The position is incremented, and the right operand is evaluated by calling parse_expression again, but the precedence is now set to the operator's precedence plus one, to ensure that if the next operator has the same precedence, that the left expression is evaluated first. This ensures that all operators are left-associative. Then, the left operand is set as the evaluation of the left operand, the operator, and the right operand. The algorithm then loops to the next token, until the entire tokens array is parsed, or the loop is broken. After the loop, the algorithm returns the evaluation of the expression and the position in the tokens array.

Parse Factor Function

parse_factor is a recursive function that takes in the tokens array and the current position in the array, and returns an evaluation and the current position in the tokens array.

  1. Begins by getting the current token at the current position in tokens array, and then incrementing the current position.

  2. If the current token is one of the unary operators:
    • parse_factor is called again with the new current position.
    • The first return value is evaluated with the unary operator (current token).
    • The evaluated value is returned, along with the position returned by the recursive call.
    • Note: As unary operators are handled in parse_factor, they will not need to be handled in parse_expression.

  3. If the token is an integer:
    • The function simply returns with the value of the current token, which is an integer, and the current position.

  4. If the token is an open parenthesis:
    • Call parse_expression with the tokens array, current position, and a precedence of 0 as arguments.
    • The current position should be set to the second return value (position), and should then be incremented to skip the closing parenthesis.
    • The first return value (left_operand) of parse_expression, along with the new current position is returned.

Parse Expression Function

Provided is the pseudocode for parse_expression:

parse_expression(tokens, position, current_prec)
  left_operand, position = parse_factor(tokens, position)

  while position < length_of_tokens
    token = tokens[position]
    op_prec = precedence(token.token_type)
    if op_prec < current_prec 
      // Stop parsing, return value
      break

    // Go to next token
    position += 1

    // Current precedence will be set to 1 higher than operator precedence
    // This forces left-associativity
    right_operand, position = parse_expression(tokens, position, op_prec + 1)

    // In this line, token is an operator
    left_operand = evaluate(left_operand, token, right_operand)

  return left_operand, position

Since this algorithm uses recursion, care must be taken with how the stack is used when implementing the solution.

Below is a visual representation of what the algorithm should be doing:

Evaluation

These are the actions the operators need to perform. These actions will substitute the evaluate sections in the pseudocode above. The solution is not required to have a evaluate function, the soluion may simply implement the necessary logic for each operator in the parse_expression and parse_factor functions.

The token types provided for each operator are labels to the unsigned byte representation of the operator. They can be accessed in a single instruction, e.g. lbu t0, TOKEN_PLUS

Binary Operators

Unary Operators

The tokens for arithmetic negation and subtraction are the same, as well as the tokens for addition and the unary positive operator.

Assignment

The solution for this assignment consists of a RISC-V assembly file containing four functions that will calculate the expression. The solution may contain additional functions or global variables as needed, but the four functions below are the only ones that will be marked.

Functions to Complete

Assumptions and Notes

Testing

The Code directory contains the following files:

Test cases will be provided as .txt files in the format: 

<expression>

The solution will be in .out files of the same name, in the format: 

First factor: <value-of-first-factor>Expression: <result-of-expression>

For example, a simple test case called test.txt could look like this: 

3 + 5 * 2

And its result would look like this, in a file named test.out: 

First factor: 3Result of expression: 13

To run a test, call RARS with the path to the test file, like so:

rars parser.s nc pa path/to/test.txt

The nc argument is required to hide the copyright notice, which can interfere with the output.

Resources

Marking Guide

Assignments too short to be adequately judged for code quality will be given a zero for that portion of the evaluation. Marks are commonly lost in the program style section, common deductions include register calling convention errors, incomplete register usage sections, and unreadable uncommented code.

This assignment will be marked solely on the functions implemented, and the program style of the implemented code.

Submission

There is a single file to be submitted for this lab: